Introduction
Ver. all 2013 2016 2019 2021 365
Excel(エクセル)での偏差や分散の計算方法や関数について説明します。これらの言葉は偏差値を求める場合などに使用しますね。
なるだけ公式や難しい話は抜きにして、文系の方でも大丈夫なように簡単に説明します。
ここでは、それぞれの言葉の意味と関数の紹介がメインですので、偏差値の求め方を知りたい方は、下のリンク先をご覧ください。


なるべく簡単な説明が助かるにゃー
偏差とは
偏差とは・・・データとその平均値がどれだけ離れているかを示す(平均値との差)
例えば
「100」 「80」 「40」 「20」
という4つの数値があったとします。
この場合の各数値の偏差を考えてみましょう。
まず、全体の平均値を出します。
4つの数値の平均は
(100+80+40+20)÷4=60
になります。
偏差は、平均値との差になるので、
「100」・・・100-60=40
「80」・・・80-60=20
「40」・・・40-60=-20
「20」・・・20-60=-40
これが各数値の偏差になります。
分散とは
分散とは・・・複数の数値のばらつきを表す
身長150cm、170cm、190cmの3人がいた場合は、数字の分散は大きくなります。
身長165cm、170cm、173cmの3人がいた場合は、数字の分散は小さくなります。
先ほどの身長の例でやってみると、
最初の3人の平均は(150+170+190)÷3=170
それぞれの偏差は
150-170=-20 170-170=0 190-170=20
それぞれを2乗すると
(-20)2=400 (0)2=0 (20)2=400
さらに平均を出すと
(400+0+400)÷3=266.666・・・
つまり3人の分散は約267ということが分かります。
分散を求める関数
エクセルには分散を求める関数があるので、使ってみましょう。
下の表の青枠部分の分散を出します。
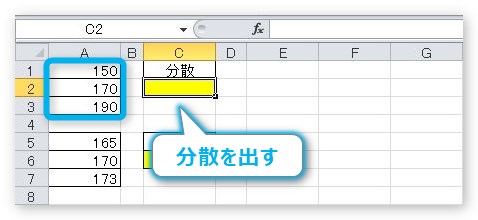
関数を入れるセルをクリックして[関数の挿入]ボタン。
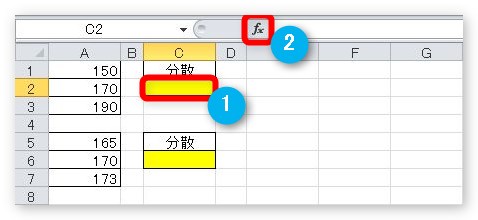
一覧から[統計]を選び、
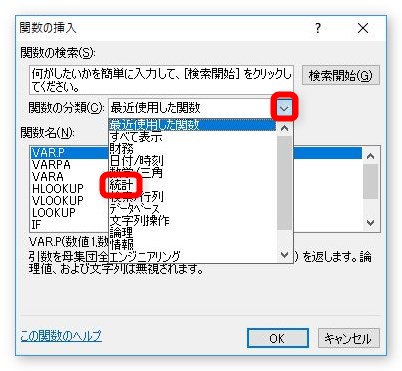
[VAR.P]関数を選びましょう。
※エクセル2007までは、VARP関数
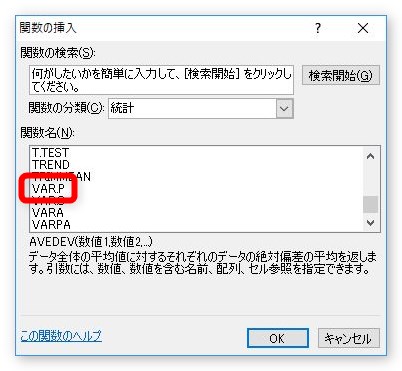
引数に分散を出したい3つの数値を選択して、[OK]をクリックすると、
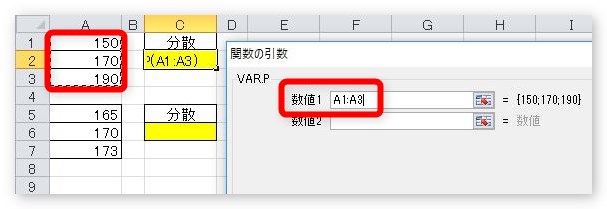
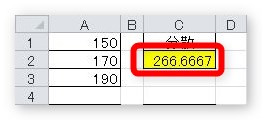
結果が表示されます。
ついでに、もう一つの方も関数を使用して出してみると、約10.89になりました。
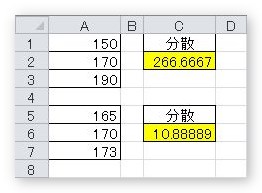
つまり、下の方がばらつきが少ないということです。確かにそうですね。
さて、今回は[VAR.P]関数を使用して分散を求めましたが、先ほどの関数選択画面を見ると、似たような関数があるのに気付きます。
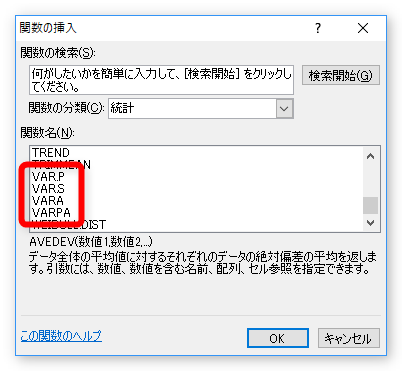
それぞれの関数の特徴を簡単に説明します。
- VAR.P関数・・・母集団全体から分散を計算する(文字列のセルは無視する)
- VAR.S関数・・・母集団を標本として予測した分散を計算する(文字列のセルは無視する)
- VARA関数・・・母集団を標本として予測した分散を計算する(文字列のセルも含める)
- VARPA関数・・・母集団全体から分散を計算する(文字列のセルも含める)
「標本として」という言葉が出てきますが、これは選択した範囲のデータをサンプルとして扱い、予測も含めた計算をするという事。
全てのデータが揃っている場合は予測は必要ないと思いますので、VAR.P関数を使用することが多いのではないでしょうか。文字列を含めることも無いと思いますし・・・。
ここでちょっと待ったです。
実はVAR.P関数を使うならば「VARP関数」を使用した方が良い職場があるかもしれません。途中に「.」ピリオドがあるか無いかの違いですが、VAR.P関数はバージョン2010から名前が変更された関数で、2007以前はVARP関数でした。
下の関数はエクセル2010のバージンアップ時に名称が変更されています。
- VARP関数 → VAR.P関数
- VAR関数 → VAR.S関数
自社や取引先の会社が、古めのPCを使用している可能性がある場合、互換性を考えてVARP関数を使用した方がよいかもしれません。
「え?さっきの関数選択の画面にVARPという名前が見当たらなかったけど・・・」
そう。[関数の分類]で[統計]を選ぶと、先ほどの画面のように旧バージョンの関数が表示されません。
[すべて表示]を選び、関数全てを表示すると、下のように表示されます。
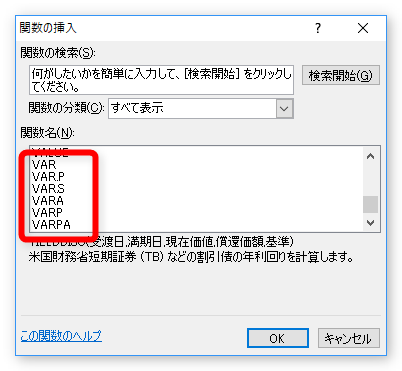
分散を求めたい時は、こちらの画面から「VARP関数」を選択することも可能です。
まとめ
偏差と分散の説明でした。そのまま偏差や分散を仕事で使用する機会がある方は少ないかもしれませんね。
分散は関数で求めることができますが、同じ関数で名称が新しくなっている場合は、互換性を考えて、あえて古い名称を使用することも考えましょう。

ZZZ


