Introduction
Ver. all 2016 2019 2021 2024 365
平均値と中央値と最頻値の違いは何だろう?また、エクセルでそれらを使用する場合の関数やグラフは?
それらを簡単に説明します。

中央値と平均値の違いは大切みたいだにゃ
平均値、中央値、最頻値の違い
それぞれを、一言であらわすと以下のようになります。
- 平均値・・・すべてのデータを足して、個数で割った値
- 中央値・・・データを大きさ順で並べた時の中央に位置する値
- 最頻値・・・一番出現する回数が多い値
これらの違いを具体的に説明していきます。
20人のクラスで小テストを行いました。
100点満点のテスト結果が下の表です。
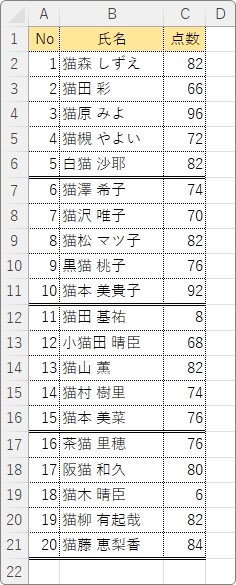
この結果で平均値、中央値、最頻値を調べると、下のような結果になりました。
- 平均値・・・71.4
- 中央値・・・76
- 最頻値・・・82
最初に「最頻値」からいきましょう。
こちらは単純に一番出現回数が多い数値のことです。今回の表では「82」点の人が4人いて、これが一番多い点数です。
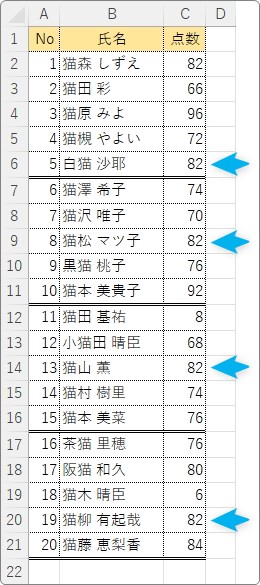
「最頻値」は漢字そのまま、「頻度が最も多い値」なので分かり易いですね。
同じデータが出現する頻度を調べるため、データ量が多い場合に有効です。
また、Excelで同じ頻度のデータが複数存在した場合は、最初に出現したデータが結果として表示されます。
では、次に平均値と中央値を考えてみましょう。
どちらも「真ん中の値」という意味では似ている数値のはずなのですが、今回はかなり異なっています、
- 平均値・・・71.4
- 中央値・・・76
「4.6」の開きがあります。
理由は、全体的に高得点の試験だったのに、2人だけ低い点数がいたからです。
「猫田」くん8点。「猫木」くん6点。
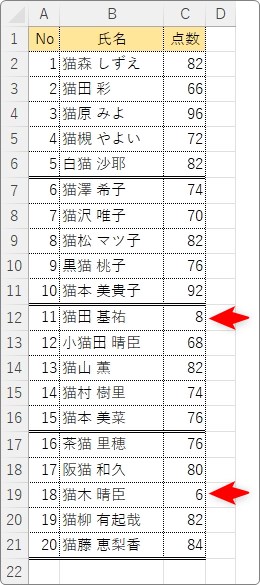
これにより、2つの結果に開きが生じてしまいました。
- 平均値・・・すべてのデータを足して、個数で割った値
- 中央値・・・データを大きさ順で並べた時の中央に位置する値
「今回の試験の点数の難しさはどれぐらいだったかな?」と分析したい時には、どちらが良いでしょうか。
他と比べて極端に点数の低い2人は考えずに、平均ではなく中央値で考えた方が参考になりそうです。
ここで、中央値と平均値の使い分けについてまとめておきます。
良い点
- 平均値・・・全体の数値の比較ができる
- 中央値・・・極端に大きい数値や小さい数値の影響を受けない
悪い点
- 平均値・・・極端な数値も結果に含まれてしまう
- 中央値・・・全体の数値の比較には向かない
ということになります。
極端な数値も含めるべきかどうか
こちらを考えて平均値と中央値を使い分けるのが良いでしょう。
また、両方算出して見比べるのがベストな場合も少なくないはずです。
平均値、中央値、最頻値の関数
Excelでは、中央値、平均値、最頻値を関数で簡単に算出できます。
それぞれの関数名は、
- 平均値・・・AVERAGE関数
- 中央値・・・MEDIAN関数
- 最頻値・・・MODE関数
設定する引数は、3つの関数全てがデータ範囲を指定するだけです。
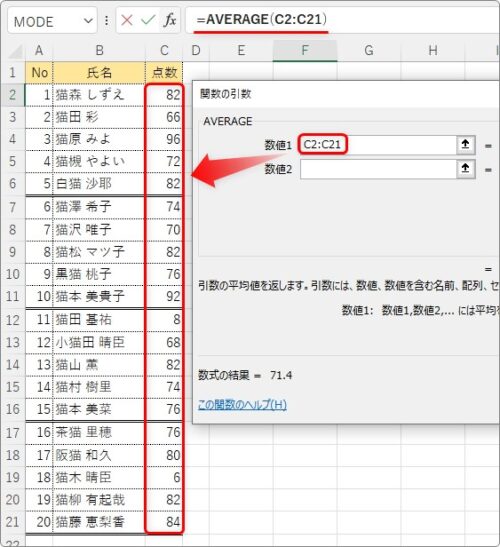
関数名を覚えておくだけで簡単に使えますね。
平均値、中央値、最頻値が分かるグラフ
それぞれの値をグラフで確認したい場合におすすめのグラフを紹介します。
平均値、中央値、最頻値を追加する
通常の棒グラフに平均値などを追加する機能はExcelにはありません。
そのため、元の表に必要なデータを追加して、そのデータを含めた複合グラフを作成します。
※今回は平均値の例で説明しますが、中央値や最頻値の場合はAVERAGEをMEDIAN、MODEに変更するだけです。
例えば下の表から作成した
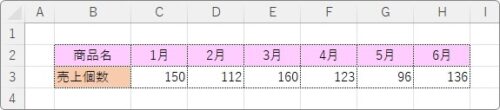
集合縦棒グラフに、
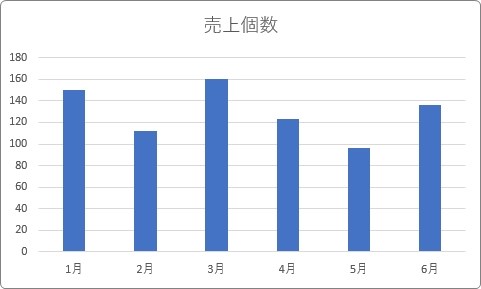
平均となる横線を追加したい場合は、元データの下に平均値を追加します。
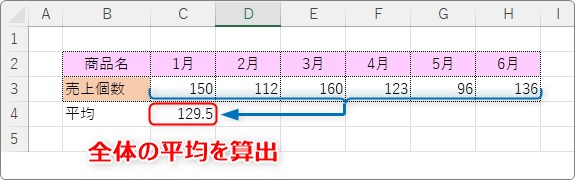
使用するのは、AVEREGE関数。
※後で、右側に式をコピーするので、平均の指定範囲に$記号を付けて絶対参照にするのを忘れないようにします。
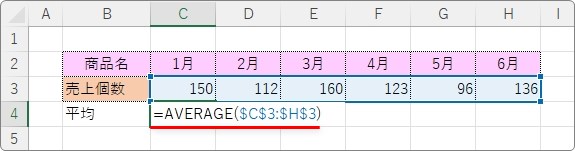
その式を右にコピーして、
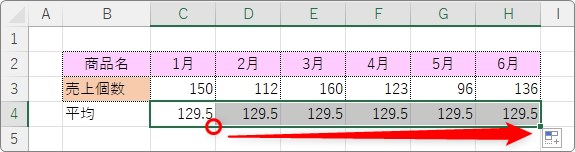
全ての場所に平均値を表示するようにします。
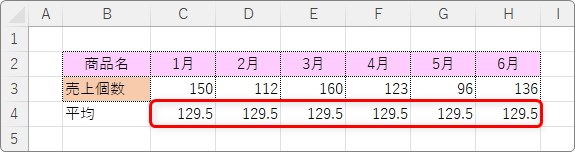
準備できたら、全体を選択して、
[挿入]タブ → [おすすめグラフ]をクリック。

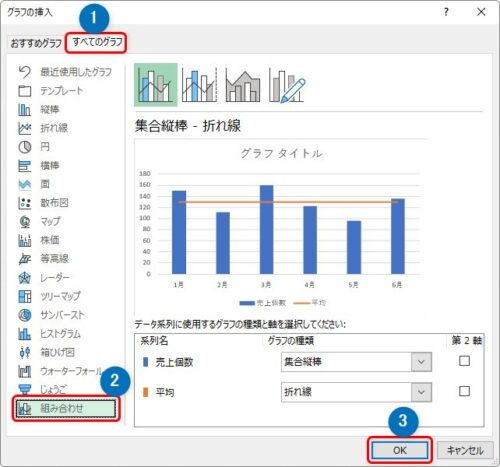
[すべてのグラフ]タブに移動 → 左側で[組み合わせ]を選択 → [OK]。
これで縦棒と平均の折れ線が組み合わされた複合グラフが作成されます。
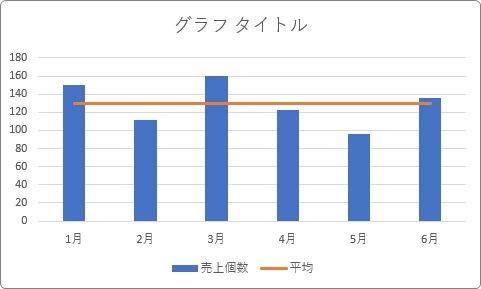
複合グラフの作成画面は、グラフ作成後も[グラフのデザイン]タブ → [グラフの種類の変更]をクリックすると再度表示できますよ。

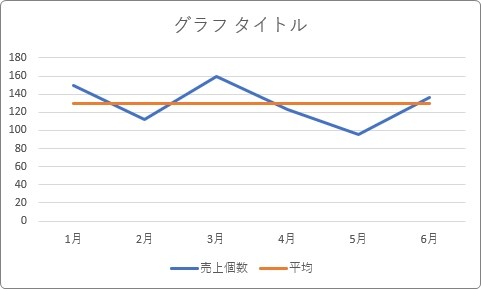
折れ線と折れ線の組み合わせにすることも、
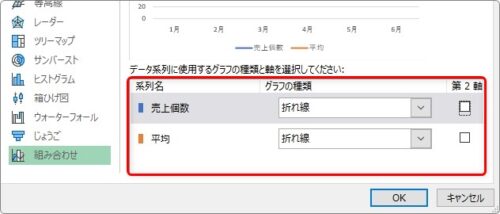
可能です。
もし、下のような形の表であれば、右側に平均データを追加します。
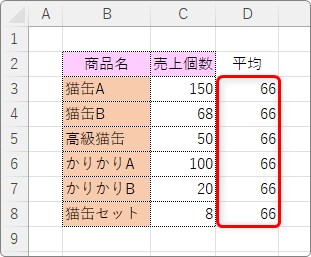
そして、追加データを含んで選択し、
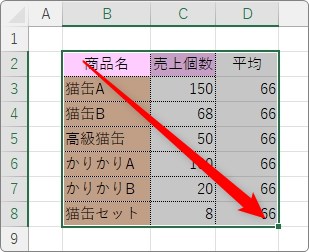
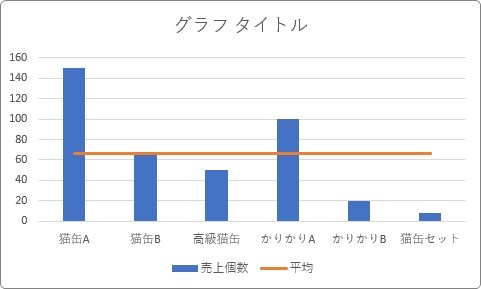
先ほどの手順で縦棒と折れ線の複合グラフを作成します。
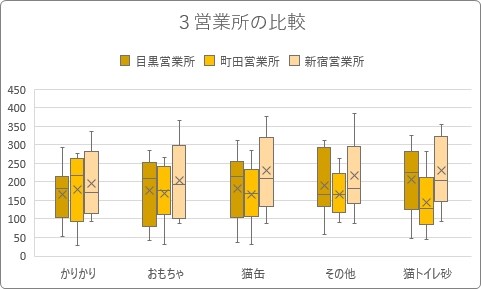
データの分布や中央値を見比べるのに便利な箱ひげ図
複数データの分布やばらつきを比較する時に便利なのが箱ひげ図です。
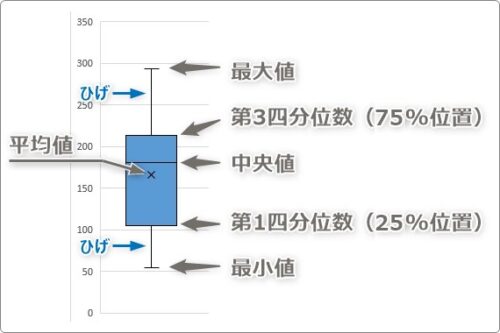
グラフの見方は下の図を参考にしてください。
それぞれ、中央値や平均値を表示できるのがポイントです。
作成に関しては、少し注意点などありますので、下のリンク先を参考にしてください。

頻度を確認するヒストグラム
ヒストグラムとは頻度を表示する棒グラフです。
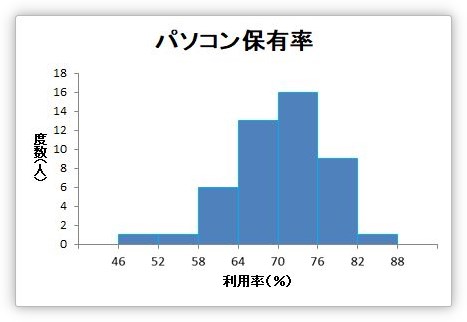
ある程度の区分で分けて、データをカウントすることで、データの散らばり具合を見ることができます。
「この辺りの数値では、どれぐらいのデータが存在するのかな?」
というのが分かります。
ヒストグラムに関しては、下のリンク先をご覧ください。

まとめ
最後にポイントをまとめておきます。
- 平均値・・・すべてのデータを足して、個数で割った値
- 中央値・・・データを大きさ順で並べた時の中央に位置する値
- 最頻値・・・一番出現する回数が多い値
- 平均値・・・AVERAGE関数
- 中央値・・・MEDIAN関数
- 最頻値・・・MODE関数
やはり、注意したいのは平均値と中央値の違いだと思います。
データ分析をする際に、どの値が必要なのか考える必要があります。
適切なデータで適切な分析ができるように、それぞれを使い分けたいところですね。

グラフの使い分けも大切だにゃ


